The image above can be found from various sources on the internet and I am not sure of the origination.

Hello, my name is Rick and I am in search for gig as a developer :). I am familiar with the MERN stack (MongoDB, Express, React, and NodeJs), HTML, and CSS. I have been deeply immersed in these technologies since January 2021.

After a brief hiatus with Covid (put me out for 3-4 days), I started diving into data structures with Colt Steel's course on Udemy, which can be found here. The purpose of these blogs are to essentially document my learning journey.

What is Big O notation?

Big O notation is a mathematical representation of how efficient an algorithm performs during run time.

What is an Algorithm?

A sequence of steps (instructions) to solve a clearly defined problem.

In programming, these set of instructions are commonly defined inside of functions. Take for example the following problem:

Let's write a function that takes in a number and adds the total of 1 to that number, to include the number. If the input is 3, add 1 + 2 + 3 to get a result. Below are two examples of an algorithms that solves this problem:

a. O(n) (linear time)

function addSum(n){
let total = 0;
for (let i = 1; i <= n; i++){
    total += i;
  }
return total;
}

b. O(1) (constant time)

function addSum(n){
return n * (n+1) / 2
}

Time Complexity

Given the two examples above, let's focus on speed, the time it takes to run, or what's called 'time complexity' When the input data is small, how the algorithm runs does not matter as much . However, as the size of the input grows, it does start to matter as this could cause our code take longer to finish the operations.

First, look at example b, there are 3 operations present. 1 multiplication, 1 addition, 1 division. Therefore, it doesn't matter what n is, the number of operations stay the same. We would call this O(1) - Also known as "constant time".

Example a shows a function with linear time complexity, or O(n). As the input grows, so does the number of operations, in a proportionate way.
(Each time a loop runs, the number of operations continue to grow) The result is a linear line on the graph representing the number of operations.

In another example, let's look at a function that has a nested loop.

O(n²) or O(n^2) (quadratic time complexity)

function print(arr) {
    for (let i = 0; i < arr.length; i++) {
        for (let j = 0; j < arr[i].length; j++) {
              console.log(arr[i][j]);
        }
      }
  return;
}

Big O quadratic time complexity, or O(n²), represents how time may exponentially grow as the number of inputs grow, which is an even worse case for the performance of an algorithm. Notice that the line representing this in the graph above moves up at an even steeper rate.

Simplifying the Big O expressions

O(1)

function addSum(n){
return n * (n+1) / 2
}

If you look at the function above and count the number of operations you may come to the conclusion that the big O notation would be O(3), but since it is constant, we simplify it to O(1).

O(n)

function addSum(n){
let total = 0;
for (let i = 1; i <= n; i++){
    total += i;
  }
return total;
}

For each n, there are 5 operations/assignments present and out side of n, there are 2 constant operations/assignments present. Therefore we can come up with something like 5n +2, which we simplify to O(n). As n grows, the run time grows proportionally.

Always simplify the expressions to the highest runtime variable. (Constants and smaller terms don't matter).

• O(623) = O(1)

• O(12n +3) = O(n)

• O(2n² + 2n + 3) = O(n²)

The take-away thus far

• O(1) is great and difficult to achieve, especially as algorithms become more complex.
• O(n) is not as good but ok.
• O(n²) should be avoided if possible and would perform the worse out of the three.

Auxiliary space complexity

Space taken up by the algorithm only. (not including the space taken by the inputs)

Space Complexity

• All primitive values except strings are constant space O(1)

• Strings require O(n) space (where n is the string length)

• Reference types (arrays and objects) are generally O(n) (where n is the array length or number of keys in obj)

What is the Big O notation for the following functions based on space complexity?

function logUpTo(n){
for (var i =1; i<= n; i++){
       console.log(i)
  }
}

This would be O(1). No matter how large n is, the variable i holds a primitive value and the space in memory is unaffected.

function onlyElementsAtEvenIndex(array) {
    var newArray = Array(Math.ceil(array.length / 2));
    for (var i = 0; i < array.length; i++) {
        if (i % 2 === 0) {
            newArray[i / 2] = array[i];
        }
    }
    return newArray;
}

This would be O(n). The variable i is a primitive value and is unaffected by the array passed in. However, newArray size is determined by the argument passed in (array). This one seems like sort of a trick question. First of all, Math.ceil() ? lol If you check this function out it's setting an empty array to half the length of the array passed in. Then, if the index (to include 0) is divisible by 2, then we set each index of the new array ( i / 2) to those values from the even indexes from the array passed as an argument. Either way you manipulate the array here, the array passed in effects the size of memory in the newArray. O(n).

Logarithms

What are logarithms?

• The inverse of exponentiation

Ok, so what's that mean?

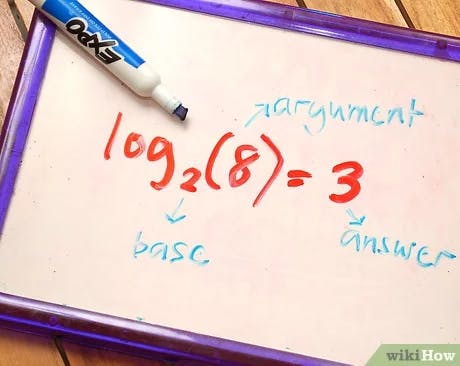
source: wikihow.com/Understand-Logarithms

The picture above shows a logarithm. You can look at this a 2, to what power, equals 8? The Base does not have to be 2, but binary logarithms are the most common. As a general rule, you can think of a binary logarithm of a number is how many times that number can be divided by 2 before getting a value that's less than or equal to one.

To find out more about logarithms go here.

Where do these logarithms show up?

• Certain searching algorithms have logarithmic time complexity.

• Efficient sorting algorithms involve logarithms.

• Recursion sometimes involves logarithmic space complexity.

Final thoughts

My resources for this was Colt Steel's course on Udemy, which can be found here. I'm essentially taking notes during the video lecture. Big O notation is import to understand, not only when writing code for optimal performance, but also this understanding may come in handy during a job interview. If you see any discrepancies, or like to add to anything mentioned in this article, please feel free to comment.